
Is, we can easily choose the correct solution. Positive angles start on the positive x-axis and.
If we know the quadrant where the angle It is useful to note the quadrant where the terminal side falls. Notice that we used only the positive root because $15^)$ is therefore positive. Recall that different signs are applied to trigonometric functions that fall in each of the four quadrants (according to the mnemonic rule "A Smart Trig Class"). The unit circle, and the sine values are negative between $\pi$ and $2\pi$, which correspond to the values of the sine function in quadrants III and IV on the unit circle. Notice how the sine values are positive between $0$ and $\pi$, whichĬorrespond to the values of the sine function in quadrants I and II on. Example 1 : Determine the following pairs of angles are coterminal. The four quadrants are labeled I, II, III, and IV. Give the quadrant of the angle, if applicable. Label these quadrants to mimic the direction a positive angle would Defining Trigonometric Functions on the Unit Circleĭivide the coordinate plane (and the unit circle, since it is centered at the origin) into four quarters called quadrants. The four quadrants of a Cartesian coordinate system. A reference angle is an acute angle (<90) that can be used to represent an angle of any measure. Point $(0,-2)$ is on the y-axis and also not in a quadrant. Knowing the values of cosine and sine for angles in the first quadrant allows us to determine their values for corresponding angles in the rest of the quadrants in the coordinate plane through the use of reference angles. Point $(4,0)$ is on the x-axis and not in a quadrant. The third quadrant has both negative x and y coordinates. For any angle in quadrants II, III, or IV, there is a reference angle in quadrant I. In the second quadrant with the same sine value. For any given angle in the first quadrant, there is an angle. Reference angles in quadrant I are used to identify which value any angle in quadrants II, III, or IV will take. In quadrant II, “Smart,” only sine is positive. In the fourth quadrant, Cos is positive, in the first, All are positive, in the second, Sin is positive and in the third quadrant, Tan is positive.Examples of quadrants in the following topics:. In the first quadrant, the values for sin, cos and tan are positive. The angles which lie between 0° and 90° are said to lie in the first quadrant. How do you know what quadrant a sin is in? Angles coterminal with these angles are, of course, also quadrantal. 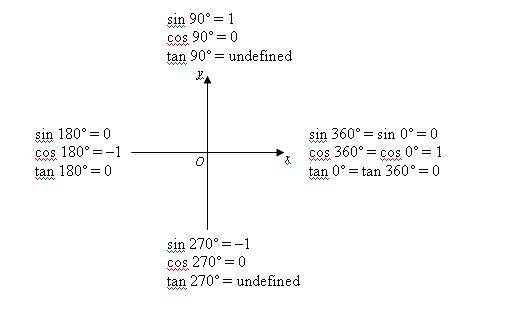
Examples of quadrantal angles include, 0, π/2, π, and 3π/ 2. What is a quadrant angle?ĭefinition A quadrantal angle is an angle in standard position whose terminal ray lies along one of the axes. The quadrants are numbered I, II, III, and IV as shown on the grid below. The coordinate axes divide the plane into four regions called quadrants.

The first number in an ordered pair is the x-coordinate. Since is between and, it is a second quadrant angle. When the angle is between and, the angle is a second quadrant angle. An angle can be located in the first, second, third and fourth quadrant, depending on which quadrant contains its terminal side. The coordinate plane is divided into four regions, or quadrants. How do you find the quadrant of an angle? It must be less than 90 degree, and always positive. The figures, a, b and c below, show these relations for the angles x whose terminal side falls in the second, third or fourth quadrant. In other words, the reference angle is an angle being sandwiched by the terminal side and the x-axis. Values of trigonometric functions, of any angle greater than 90° (p/2) can be expressed by the corresponding value of the function of an angle from the first quadrant. Reference Angle: the acute angle between the terminal arm/terminal side and the x-axis. But then I remember that, on the unit circle, the sine of an angle is given by the y -value of the point at which the terminal side of the angle (that is, the hypotenuse of the underlying triangle) crosses. If the terminal side of the angle is in the 3rd quadrant, we take 180 degrees and subtract it from the angle measure. They havent given me an angle measure or even a quadrant, and they want a trig-ratio value when all theyve given me is half of a point.
How do you know what quadrant a sin is in?įinding Reference Angles Example 1: Find the reference angle for 150 degrees. How do you find the quadrant of an angle?. 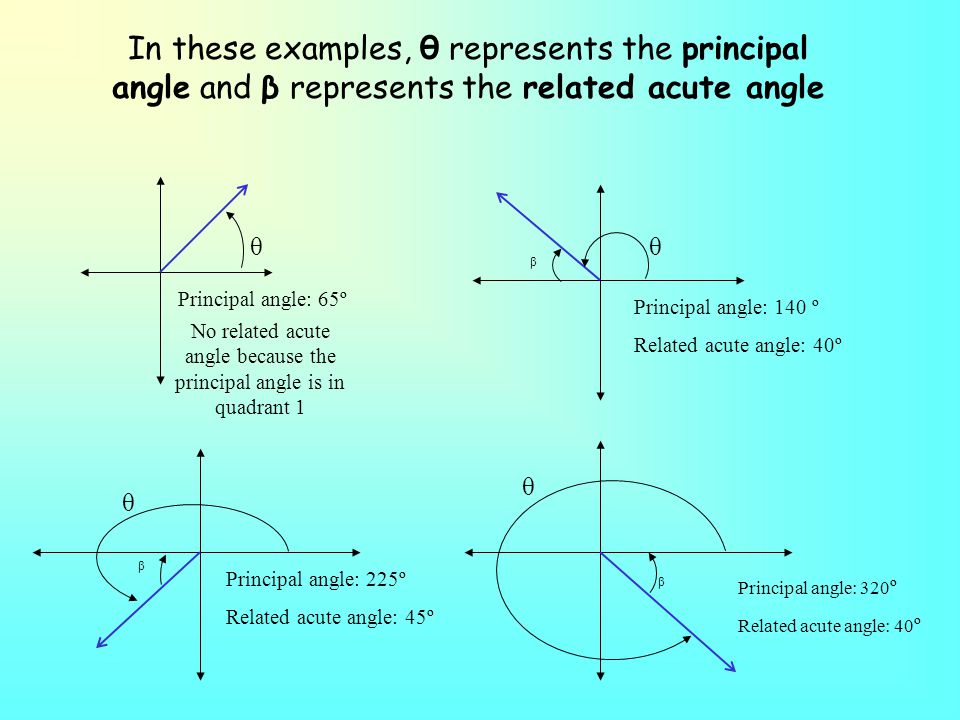
This indicates that it is an even function. How do you find the reference angle of a fraction? It is easy to calculate secant with values in the unit circle.
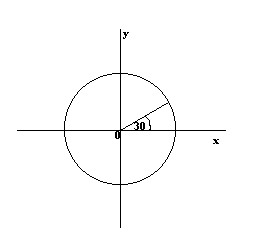
How do you find the reference angle of 5pi 3?. How do you find the reference angle of a right triangle?. What is the symbol for reference angle?. How do you find a negative reference angle?.







 0 kommentar(er)
0 kommentar(er)
